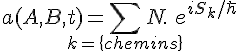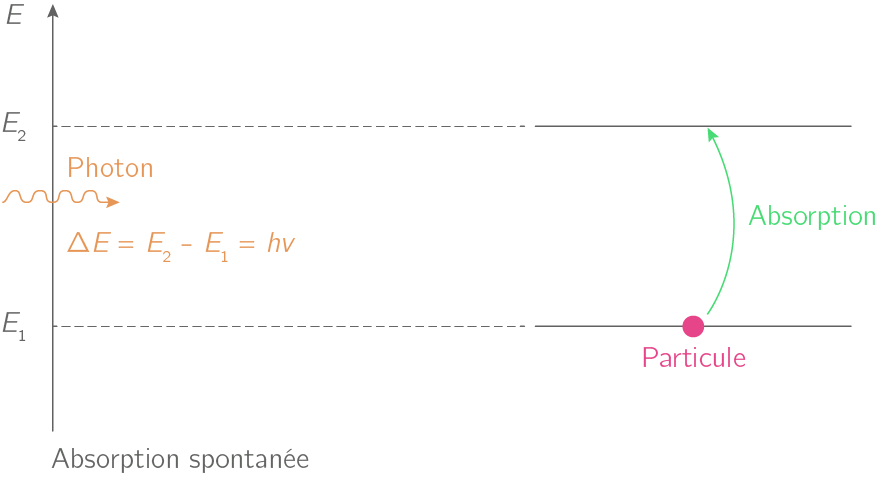Les expériences déroutantes de la physique
quantique:
La mécanique quantique, étudie le monde du
microscopique des atomes, molécules et des particules qui les composent.
Les théories de la physique quantique se sont développées progressivement au
début du 20ème siècle. Jusqu'à présent, elle n'a jamais été mise à défaut, elle
est très précise et paradoxalement repose sur des probabilités
mathématiques dont Ludwig Eduard Boltzmann (né le 20 février 1844 à Vienne)
physicien et philosophe a ouvert la voie (physique statistique).
Certains effets sont spectaculaires, mystérieux, surprenant et nous obligent à
repenser notre vision du monde.
1. Le principe de superposition
Quand on étudie le mouvement des objets du quotidien, par exemple un caillou que
l'on jette, on considère des quantités bien définies : sa vitesse, sa position,
sa vitesse de rotation ou son énergie (mécanique classique).
Nous pouvons alors connaitre très exactement ces
quantités. A un instant t donné, le caillou est dans un état bien défini.
Pour les objets quantiques, tout change ! En effet, les particules peuvent être dans
un mélange de plusieurs états. C'est fou mais, cela veut dire qu’une particule
peut posséder à la fois deux vitesses, ou être à deux ou plusieurs endroits
différents à la fois. On parle alors d'état de superposition ou du principe de superposition.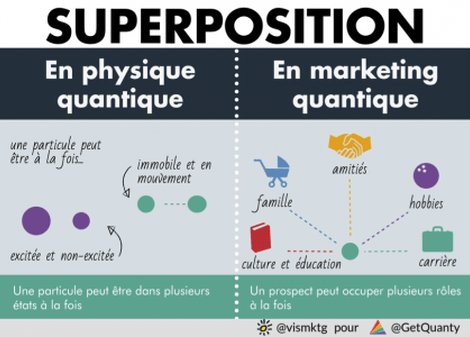
Les physiciens ont une notation bizarre pour désigner ça, il décrivent les états
avec des sortes de crochets comme celui-ci |> +-|>, et pour superposer des
états, ils les additionnent.
D'où le fameux "chat de Schrödinger", qui serait à
la fois mort et vivant, soit
|Chat> = | Mort > + | Vivant >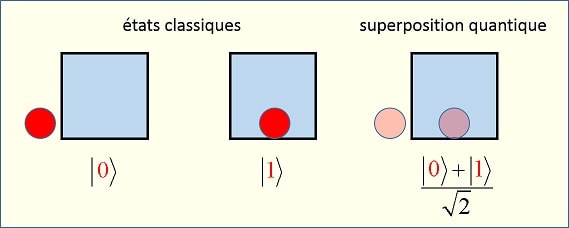
Finalement, en physique quantique tout est probabiliste et étrange!
2. L’indéterminisme de la mesure:
A. Einstein: "Dieu ne joue
pas aux dés !"
Si nous revenons à notre caillou lancé, nous pouvons connaitre avec plus ou
moins de précision sa vitesse et sa position. Nous pouvons même vérifier nos
calculs avec des instruments qui eux mêmes possèdent une certaine précision ou
incertitude sur la mesure dont il faudra tenir compte.
Passons dans le monde quantique et voyons comment cela se traduit avec un
électron qui se déplace entre 1500 km/h et 2500 km/h soit
|électron> = |1500 km/h > + |2500 km/h >
Quelle vitesse de l'électron va-t-on mesurer ? 1500 km/h ? 2500
km/h ? ou la moyenne? A vrai dire impossible de le déterminer et de connaitre à
l'avance le résultat. Il est purement probabiliste. De plus, même si 50% pour 1500km/h
et 50% pour 2500km/h semble très logique, la réalité est tout autre car il peut y avoir d'autres variantes où les états sont mélangés tels que
par exemple:
(1/4) | 1500 km/h > + (3/4) | 2500 km/h >
Ce qui veut dire que l’électron est 3 fois dans l’état 2500km/h et une fois dans
l'état 1500 km/h.
En réalité, la nature n'est pas "déterministe" (on ne peut pas prédire en
physique quantique ce qu'il va se passer!). Les résultats dépendent purement du
hasard et ne tiennent pas compte de la logique!
Il y a un "indéterminisme
fondamental", les résultats des mesures sont le fait du hasard, il est donc est impossible de
les prévoir.
3. La dualité onde-corpuscule
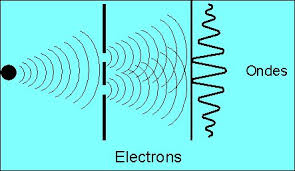 En mécanique quantique,
nous pouvons superposer les états et un objet quantique peut se trouver dans plusieurs endroits à la
fois, c'est la surperposition. La particule peut être dans une infinité
d’endroits à la fois, il peut y avoir une infinité
d’états différents.
En mécanique quantique,
nous pouvons superposer les états et un objet quantique peut se trouver dans plusieurs endroits à la
fois, c'est la surperposition. La particule peut être dans une infinité
d’endroits à la fois, il peut y avoir une infinité
d’états différents.
Du coup, il peut y avoir avoir une certaine probabilité que la particule
soit un peu plus dans un état que dans un autre dans un espace donné: Ψ =(x,y,z)
.
Rappel mathématique:
La fonction d'onde est une amplitude de
probabilité de présence et le
carré de sa norme qui représente la densité volumique de probabilité de
présence de la particule.
C'est une propriété
ponctuelle. En chaque point de l'espace, on peut calculer cette
densité volumique à partir de l'expression de la fonction d'onde.
Si on veut calculer la probabilité de
présence de la particule  à
l'intérieur d'un volume fini, il faut procéder à une intégration sur ce volume
de la probabilité élémentaire :
à
l'intérieur d'un volume fini, il faut procéder à une intégration sur ce volume
de la probabilité élémentaire :
Du coup, notre particule n’est plus un corpuscule localisé mais une onde qui a
pour fonction
Ψ =(x,y,z)
appelée champ de probabilités. Finalement, on ne va plus décrire notre particule comme
un objet ponctuel, mais comme une onde !
C'est Louis De
Broglie qui proposé de parler de la dualité onde-corpuscule :
les particules peuvent se comporter soit comme des
particules, soit comme des ondes. En fait cela dépend ce que l'on cherche à
observer. La lumière en est un exemple flagrant puisqu'elle est à la fois ondes
électromagnétiques et photons.
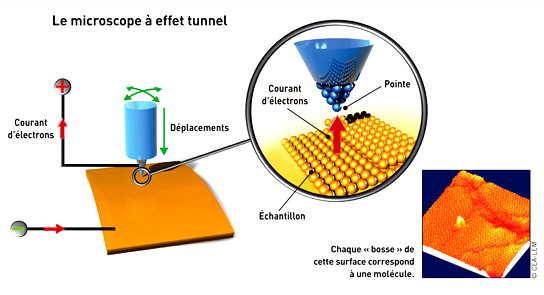
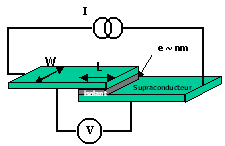
4. L’effet tunnel
Après ce qui vient de
suivre , concernant le
principe de superposition, il faut décrire les particules comme des ondes.
Si nous lançons notre caillou contre un mur, il ne va pas le traverser et va
rebondir. Mais si nous considérons qu'il s'agit d'une onde, les observations
vont être différentes. Si un électron percute un obstacle microscopique et qu'il
se comporte comme une onde, il peut arriver qu'il passe à travers l'obstacle.
Ψ =(x,y,z)
est la probabilité de trouver l’électron à
un endroit donné, même si pour notre exemple, cette probabilité est très faible
, elle n'est pas nulle et donc possible. C'est l’effet tunnel.
L’effet tunnel a d'ailleurs de nombreuses applications pratiques et expliquent
beaucoup de phénoménes.
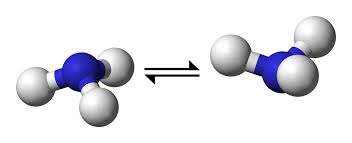
- Les molécules : NH3,l'atome
d'Azote ne peut pas passer de l'autre coté du triangle formé par les trois
atomes d'hydrogène car il est trop gros. Mais il a tout à fait le droit de se
trouver de l'autre coté. Il peut donc s'y retrouver malgré tout par "effet
Tunnel"
5. L’intégrale de chemin
Le caillou que l'on jette va suivre une direction bien définie alors qu'en
mécanique quantique, une particule peut suivre plusieurs trajectoires à la fois
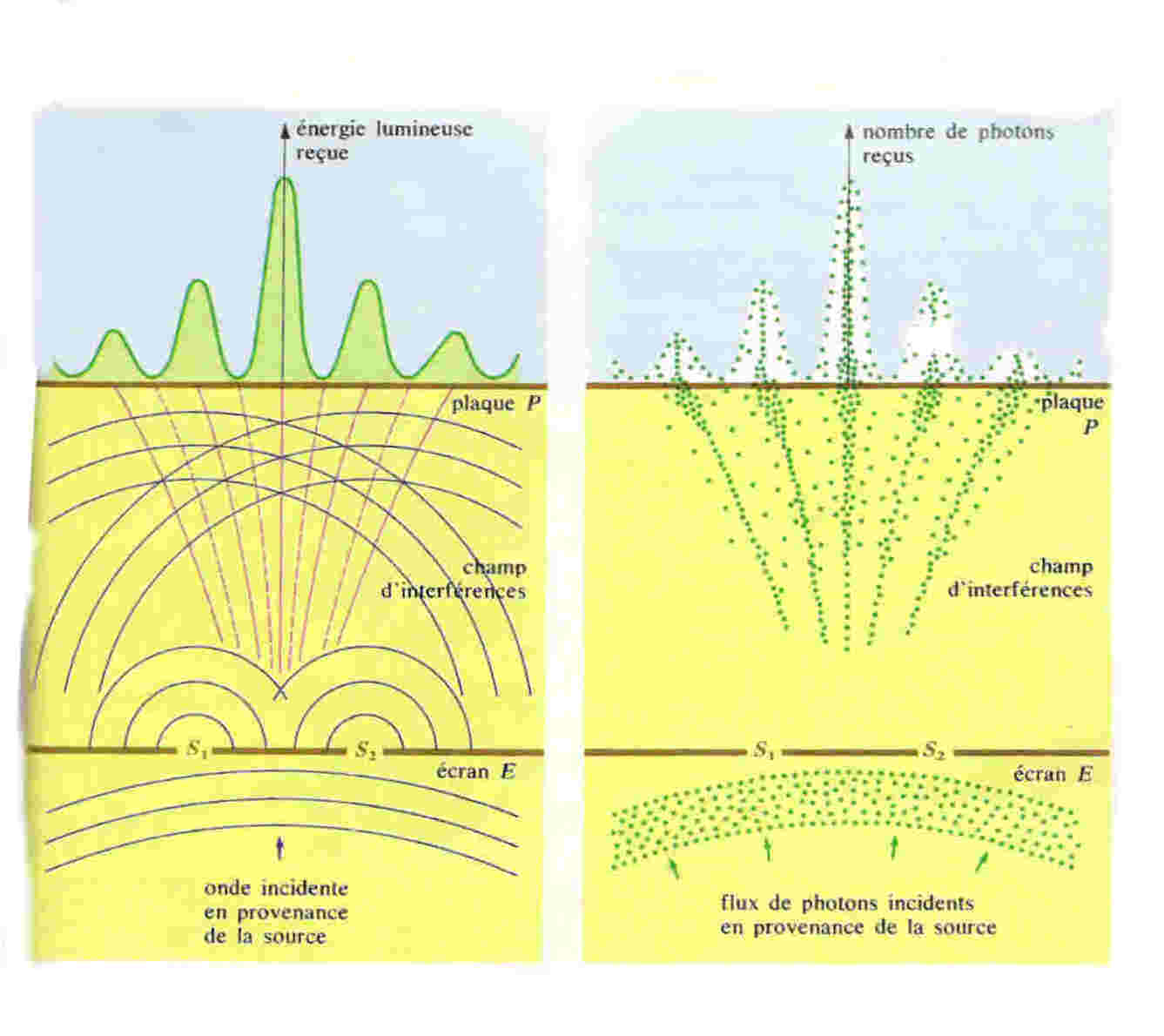
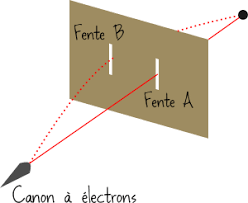
(puisqu'à plusieurs endroits en même temps!). L’illustration la plus spectaculaire de ce phénomène est celle de l’expérience
de la double fente.
Il y a une certaine (amplitude de) probabilité pour que la particule partant de
A arrive en B au bout d'un temps t. L'idée de Feynman a consisté à dire que
cette (amplitude de) probabilité était la somme des (amplitudes de) probabilités
individuelles pour tous les chemins possibles passant entre A et B et ceux avec
la même amplitude ! La seule chose qui distingue un chemin d'un autre et la
phase de l'amplitude de probabilité associée à chaque chemin.
En gros ca s'écrit :
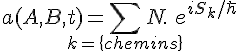
avec le même N pour chaque chemin ! et S étant l'action classique associé à un
chemin k. L'idée est que tout les chemins contribuent avec le même poids (ca
parait dingue mais ca marche) mais avec une phase différente. Cette égalité est
simplement formelle, il est difficile d'y donner un sens mathématique rigoureux,
mais les physiciens ont su lui donner une interprétation physique précise et ont
trouvé des moyens et des astuces pour calculer cette somme). Le résultat est que
toutes ces phases interférent entre elles pour redonner la fonction d'onde
usuelle qui obéit à l'équation de Schrödinger !
L’équation de Schrödinger (1925)
est l’équivalent en mécanique quantique de la loi de conservation de l’énergie :
c’est la relation fondamentale de la mécanique quantique.
Elle s’écrit : Hy =
Ey ,
où H est appelé l’opérateur hamiltonien, y ,
la fonction d’onde, et E l’énergie.
L’opérateur hamiltonien s’exprime par :
Hy = - h²
/ 2m D y + V(r).y
Où D y est
le laplacien vectoriel de la fonction d’onde :
D y = ¶ ²y / ¶ x²
+ ¶ ²y / ¶ y²
+ ¶ ²y / ¶ z²
(en coordonnées cartésiennes soit x,y et y en 3D!)
Il existe une infinité de solutions à
cette équation. Seules sont retenues celles qui ont un sens physique
c’est-à-dire qui respectent les conditions mathématiques suivantes : continue,
dérivable, uniforme (une seule valeur en un point donné de l’espace), nulle à
l’infini.
Le traitement mathématique de cette
équation appliquée à l’atome d’hydrogène fait apparaître une dépendance à trois
nombres appelés nombres
quantiques principaux n
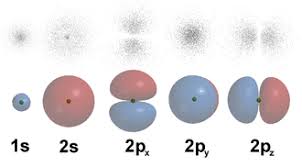
(Couches électroniques K,L,M...) , l (cases quantiques de remplissages des
électrons 1s, 2s, 2p, 3s, 3p, 3d,...) et m (spin tourne dans un sens ou
dans un autre mouvement de précession).
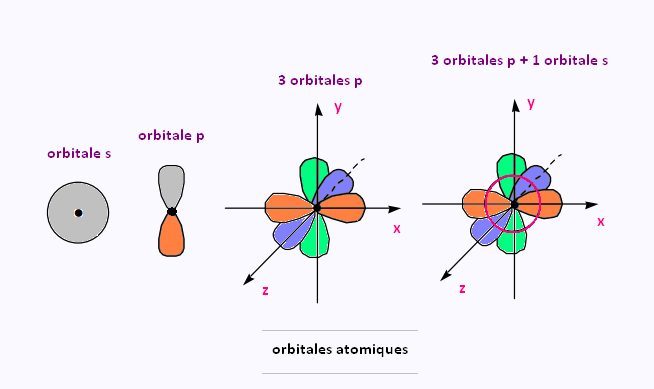
Les fonctions d’ondes solutions de
l’équation de Schrödinger sont appelées orbitales
atomiques.
Mais l'équation de Schrödinger ne peut
être résolue exactement que pour les atomes,
ions ou molécules monoélectroniques.
NB: Un opérateur hamiltonien est un opérateur mathématique possédant de
nombreuses applications dans divers domaines de la physique.
6. La quantification
De cette découverte (Planck entre autre) va découler une multitude de théorie.
Dans le monde quantique, les particules n’ont droit qu’à certaines énergies. Un
peu comme une voiture qui ne pourrait rouler qu’à une certaine vitesse et
passerait brusquement de 50 à 70 km/h sans transition! Pourquoi ?
Au niveau quantique, les particules sont des ondes et leur forme n'est pas
aléatoire. Elle est déterminée par le niveau d'énergie de la particule. Ce
phénomène s'appelle la quantification. Ces paliers d'énergie trahissent la
structure même des atomes et permettent leur modification.
La manipulation des paliers d'énergie est, par exemple, à l'origine de la
création de certaines couleurs de Led ou de lasers. En laboratoire, ces
expériences sont réalisées dans des nanoboîtes, des structures de quelques
atomes de côté. Elles permettent d'étudier la matière et d'en modifier à loisir
sa couleur, ses propriétés magnétiques, électriques etc.
Lorsqu’un atome est à son
niveau d’énergie le plus bas, il est dans son état fondamental. C’est l’état
stable de l’atome. Lorsqu’un atome est à un niveau d’énergie plus élevé, il est
dans un état excité. On appelle transition quantique le passage de l’atome d’un
état à un autre. Pour l'hydrogène (atome le plus simple puisqu'il ne contient
qu'un proton et un électron), son niveau d’énergie le plus bas est de -13.6 eV,
il est dans son état fondamental. Pour qu'il passe au palier supérieur, il faut
lui fournir de l'énergie (l'excité) mais l'atome ne pourra que prendre une
certaine énergie ici -3,4 e. Impossible de lui donner une autre énergie. D'ailleurs,
sans cela les atomes seraient instables et notre univers ne serait pas tel qu'il
est. Le surplus ou le manque d'énergie est transformé en photon qui correspond à
une longueur d'onde bien définie.
absorption et émission
Les échanges d’énergie entre les atomes sont quantifiés : ils se
font par paquets d’énergie appelés photons. L’énergie E (J) d’un photon ne
dépend que de la fréquence ν (Hz) de la radiation associée, avec h (J.s) la
constante de Planck : E = h.ν
|
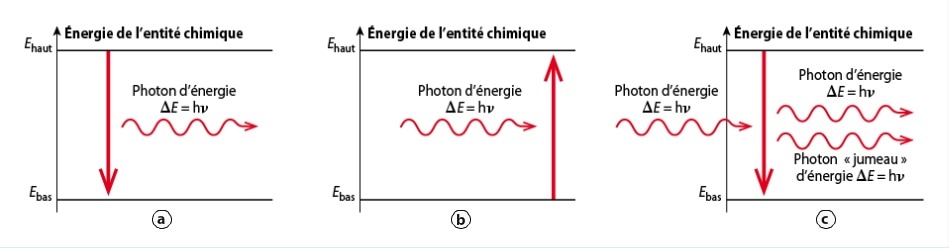
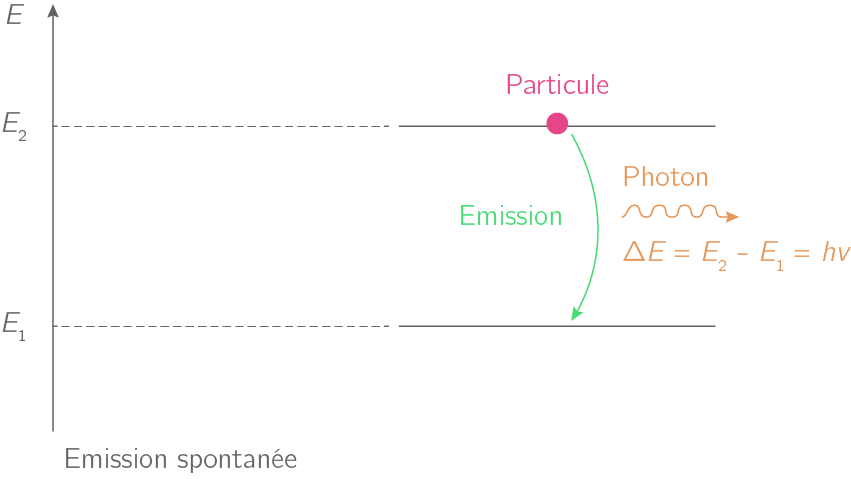
Emission spontanée a
: l’atome au niveau Ehaut revient au niveau d’énergie Ebas en émettant un
photon : Ehaut - Ebas = h.ν . Le photon est émis dans une direction
quelconque avec un déphasage aléatoire. |
Absorption b
:
un atome, initialement au niveau d’énergie Ebas peut passer au niveau Ehaut
supérieur en absorbant un et un seul photon d’énergie h.ν = Ehaut - Ebas. |
Emission stimulée c
:
Un photon peut interagir avec un atome, même si cet atome est dans un état
excité. Le photon incident n’est alors pas absorbé, mais il induit la
désexcitation de l’atome qui revient alors à son état fondamental en
émettant un photon identique au photon incident (même fréquence, même
direction et déphasage nul). Les photons produits par émission stimulée
augmentent donc l’énergie de l’onde qui interagit avec les atomes. |
Lorsqu'il y a concurrence
des deux émissions, c'est à dire que l'atome est dans un état excité, il se
désexcite spontanément pour revenir à son état
fondamental. Il émet au passage un photon. ON peut dire qu'il y a
dans une population d’atomes, beaucoup plus d’atomes sont leur état
fondamental que dans un état excité. L’émission stimulée est un phénomène très
peu probable par rapport à l’émission spontanée.
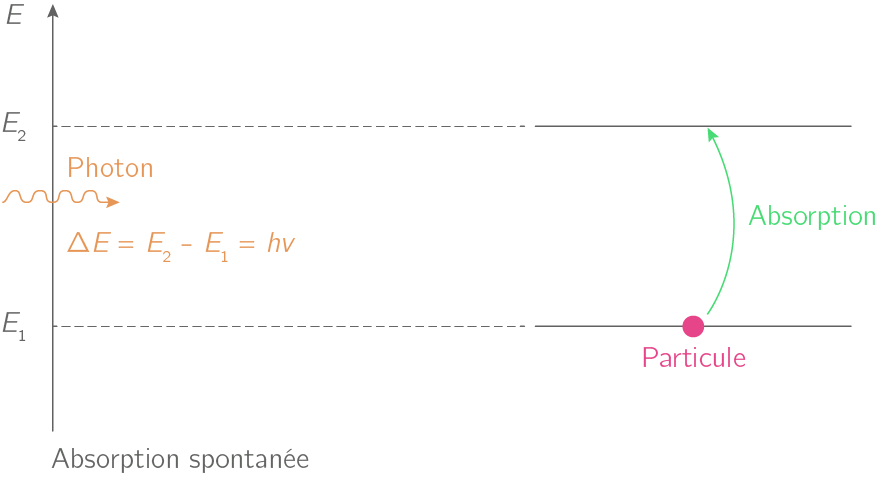
Les Applications de
cette théorie sont nombreuses.
Le laser:
Contrairement aux autres
sources de lumière qui utilisent l’émission spontanée, la lumière du laser
(Light Amplification by Stimulated Emission of Radiations) est produite par
émission stimulée.
Je vais vous résumer son
principe de fonctionnement.
Le pompage optique qu'est -de que c'est ?
L’émission stimulée est favorisée par l’inversion d'une population de photons qui consiste à
maintenir plus possibles d’atomes dans un état excité que dans l’état fondamental. Cette
situation est obtenue grâce à un apport d’énergie ; lorsque l’énergie est
apportée par des sources lumineuses, on parle de pompage optique.
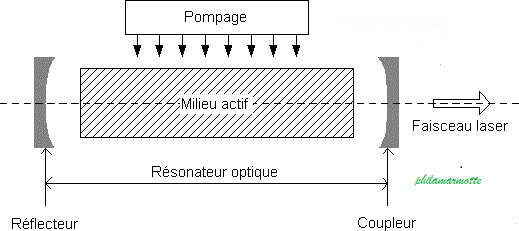
La cavité résonante
Pour amplifier davantage l’onde on peut lui faire parcourir un très grand nombre
d’aller-retour dans le milieu actif. On réalise pour cela une cavité résonante à
l’aide de deux miroirs, le coupleur étant semi-transparent.
les ondes réfléchies par les miroirs interfèrent dans la cavité. Les
interférences sont constructives si la longueur L de la cavité vérifie la
relation : 2L = k.λ
L'Oscillateur optique
L’énergie rayonnée par le laser augmente avec l’amplification de l’onde dans la
cavité résonnante. Un régime stable s’installe dans la cavité optique lorsque
l’énergie rayonnante devient égale à l’énergie fournie par le pompage optique.
L’amplitude de l’onde est alors constante. Le phénomène est analogue aux
oscillations d’amplitude constante d’un pendule entretenu. Le laser constitue un
oscillateur optique entretenu (l’énergie fournie par le pompage compense
l’énergie perdue par émission).
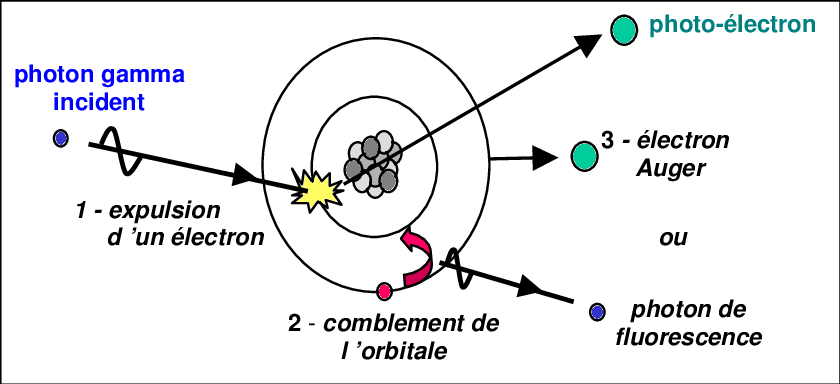
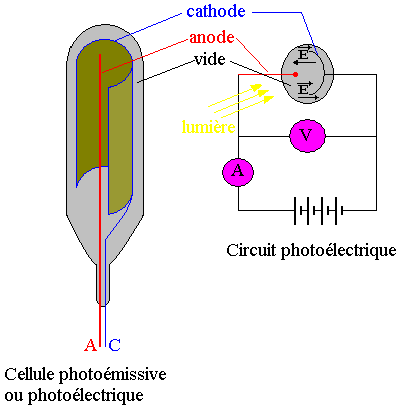
Les effets
photoélectriques (voir ma page consacrée).
7. Le principe d’incertitude de Heisenberg
Ce principe très important a été énoncé par Heisenberg découvrit qu'il existe
une limite fondamentale à la précision avec laquelle il est possible de
connaître simultanément deux propriétés physiques d'une même particule: sa
vitesse et sa position car les résultats mesurés dépendent en partie...
du hasard.
Même en reproduisant très exactement, la même expérience, les résultats
successifs ne donneront jamais strictement les mêmes valeurs. Il y a un
indéterminisme de la mesure. La superposition d'état en est un bon exemple. En
effet, la particule peut être à plusieurs endroits en même temps.
Les conséquences semblent
précéder leur cause!!! Une particule peut alors être désintégrée ou pas comme
l'expérience du chat de Schrödinger qui est à la fois mort et vivant.
Par conséquent, si nous devions mesurer une particule, on pourrait mesurer
qu'elle se déplace à plusieurs vitesse en même temps. Lorsque nous effectuons la
mesure de la vitesse, le hasard la détermine à cet instant t. Si nous refaisons
la même expérience dans des conditions strictement identique, la probabilité
d'avoir le même résultat est très incertains, c'est la décohérence quantique.
Trouver une vitesse exacte où la position exact (elle peut être à plusieurs
endroits à la fois) systématiquement est impossible. Lorsque nous voulons
connaitre la position de la particule , le hasard entre en jeu au moment de la
mesure. Ce qui est mesuré ne sera pas forcément reconductible même si dans
conditions de l'expérience sont le mêmes. Si nous voulons prévoir les résultats
des mesures, celles-ci seront toujours probabilistes.
La désintégration de particules repose sur des probabilités et est extrêmement
précise. Sauf que sur une population de particules données, nous ne serons
jamais laquelle se désintégrera mais nous savons que cela va arriver.
Dans les orbitales de Schrödinger, la particule est représentée comme un
nuage qui représente en réalité sa probabilité de présence (ici l'électron).
Lorsque nous effectuons la mesure sur ce nuage d'orbitale, le hasard
désignera l'endroit où se trouvera la particule.

Après tout ça, parlons d'ordinateur quantique et
le de téléportations!
Le 1er est déjà réalisable et le second beaucoup
complexe à réaliser à l'heure actuelle!
Dossier à suivre!!!
Un dossier sur la Théorie Janus de Jean Pierre
Petit...




 En mécanique quantique,
nous pouvons superposer les états et un objet quantique peut se trouver dans plusieurs endroits à la
fois, c'est la surperposition. La particule peut être dans une infinité
d’endroits à la fois, il peut y avoir une infinité
d’états différents.
En mécanique quantique,
nous pouvons superposer les états et un objet quantique peut se trouver dans plusieurs endroits à la
fois, c'est la surperposition. La particule peut être dans une infinité
d’endroits à la fois, il peut y avoir une infinité
d’états différents.